пришлось при построении календаря прибегнуть к системе вставки дополнительных дней, которые компенсировали бы накопившиеся за счёт дробной части тропического года дни. В юлианском календаре, введённом
Юлием Цезарем в 46 году до н.э. при содействии александрийского астронома Созигена, простые годы содержали 365 дней, високосные – 366. Таким образом, средняя продолжительность года в юлианском календаре была больше продолжительности тропического года на 0,0078 суток. В силу этого, если, например, Солнце в 325 году проходило через точку весеннего равноденствия 21 марта, то в 1582 году, когда папой Григорием ХIII была принята реформа календаря, день равноденствия пришёлся уже на 11 марта. Реформа календаря, произведённая по предложению итальянского врача и астронома
Луиджи Лилио, предусматривает пропуск некоторых високосных лет. В качестве таких лет были взяты годы в начале каждого столетия, у которых число сотен не делится на 4, а именно: 1700, 1800 и 1900гг. Таким образом средняя продолжительность григорианского года стала равна 365,2425 средних солнечных суток. В ряде стран Европы переход на новый стиль был осуществлён 4 октября 1582 года, когда следующим днём считали 15 октября. В России же новый (григорианский) стиль был введён в 1918 году, когда по постановлению СНК 1 февраля 1918 года предписывалось считать 14 февраля.
Кроме календарной системы счёта дней, в астрономии большое распространение получила система непрерывного счёта дней от некоторой начальной даты. Такая система была предложена в XVI веке лейденским профессором Скалигером. Она получила название в честь отца Скалигера Юлия, поэтому называется юлианским периодом (не путать с Юлианским календарём!). За начальную точку был принят гринвичский полдень 1 января 4713 г. до н.э. по юлианскому календарю, поэтому юлианские сутки начинаются в гринвичский полдень. Каждый день по этому счёту времени имеет свой порядковый номер. В эфемеридах – астрономических таблицах – счёт юлианских дней ведётся с 1.01.1900 г
. 1.01.1996 г. – 2 450 084-й юлианский день.
3.6. Планеты солнечной системы
В Солнечной системе девять больших планет. В порядке удаления от Солнца – это Меркурий, Венера, Земля (с Луной), Марс, Юпитер, Сатурн, Уран, Нептун и Плутон (рис. 3.6).
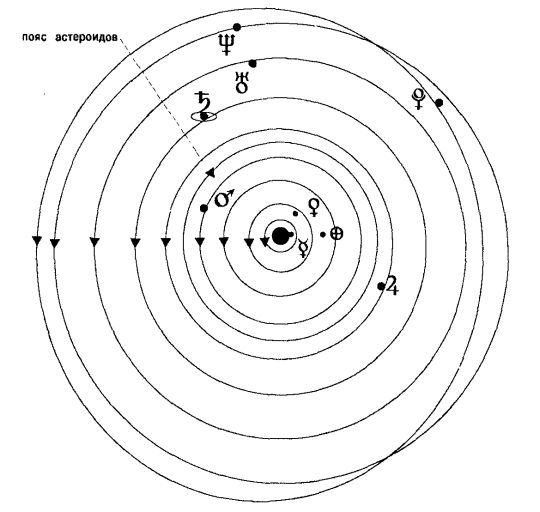
Рис.3.6. Орбиты планет Солнечной системы
Планеты обращаются вокруг Солнца по эллипсам почти в одной плоскости. Между Марсом и Юпитером обращаются малые планеты, так называемые астероиды, число которых приближается к 2 000. Пространство между планетами заполнено разреженным газом и космической пылью. Его пронизывают электромагнитные излучения, которые являются носителями магнитных, гравитационных и других силовых полей.
Солнце примерно в 109 раз больше Земли по диаметру и в 330 тыс. раз массивнее Земли, а масса всех планет вместе взятых составляет лишь около 0,1 процента от массы Солнца. Солнце силой своего притяжения управляет движением планет Солнечной системы. Чем ближе планета к Солнцу, тем больше её линейная и угловая скорость обращения вокруг Солнца. Период обращения планеты вокруг Солнца по отношению к звёздам называется звёздным, или сидерическим периодом (см. Приложение 2, Табл. 1,2). Период обращения Земли относительно звёзд называется звёздным годом.
До XVI века существовала так называемая геоцентрическая система мира Клавдия Птолемея. В XVI веке эта система была пересмотрена польским астрономом Николаем Коперником, который поставил Солнце в центр. Галилей, построивший первую зрительную трубу, прототип телескопа, на основе своих наблюдений подтвердил теорию Коперника.
В начале XVII века Иоганн Кеплер – математик и астролог австрийского королевского двора – установил три закона движения тел в Солнечной системе.
Первый закон Кеплера. Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
Второй закон Кеплера. Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади, поэтому, чем ближе к Солнцу находится планета,
тем быстрее она движется, и, наоборот, чем дальше она от Солнца, тем её движение медленнее.
Третий закон Кеплера. Квадраты времён обращения планет относятся между собой как кубы их средних расстояний от Солнца (больших полуосей их орбит). Таким образом, второй закон Кеплера количественно определяет изменение скорости движения планеты по эллипсу, а третий закон Кеплера связывает средние расстояния планет от Солнца с периодами их звёздных обращений и позволяет большие полуоси всех планетных орбит выразить в единицах большой полуоси земной орбиты.
Исходя из наблюдений движения Луны и законов Кеплера, Ньютон открыл закон всемирного тяготения. Он установил, что вид орбиты, которую описывает тело, зависит от скорости небесного тела. Таким образом, законы Кеплера, позволяющие определить орбиту планеты, являются следствием более общего закона природы – закона всемирного тяготения, который составляет основу небесной механики. Законы Кеплера соблюдаются тогда, когда рассматривается движение двух изолированных тел с учётом их взаимного притяжения, но в Солнечной системе действует не только притяжение Солнца, но и взаимное притяжение всех девяти планет. В связи с этим происходит, хотя и достаточно малое, но отклонение от движения, которое происходило бы, если строго следовать законам Кеплера. Такие отклонения называются возмущениями. Их приходится учитывать при вычислениях видимого положения планет. Мало того, именно благодаря возмущениям была открыта планета Нептун, она была вычислена, как говорится, на кончике пера.
В 40-х годах XIX века было обнаружено, что Уран, открытый В. Гершелем в конце XVIII века, едва заметно отклоняется от пути, по которому он должен следовать с учётом возмущений со стороны всех уже известных планет. Астрономы Леверье (во Франции) и Адаме (в Англии) высказали предположение, что Уран подвергается притяжению ещё какого-то неизвестного тела. Они вычислили орбиту неизвестной планеты, её массу и даже указали место на небе, где в данное время
